Project 4: A Puzzle Wrapped in an Enigma, Shrouded in Mystery

Due by: Friday, April 24, 2020 by 11:59 p.m.

If you can remember all the way back to Lab 6, we introduced the 15-puzzle, a common puzzle with 15 numbered (or otherwise ordered) tiles placed on a 4 × 4 grid, with a single empty tile. The user can move any neighboring tile to the empty location, making the previous location of the moved tile empty. The object of the puzzle is to eventually move all of the tiles around until they are numbered in ascending order, with the first tile in the upper left and the last tile empty. Below is an example of a Java GUI showing an unsolved puzzle.

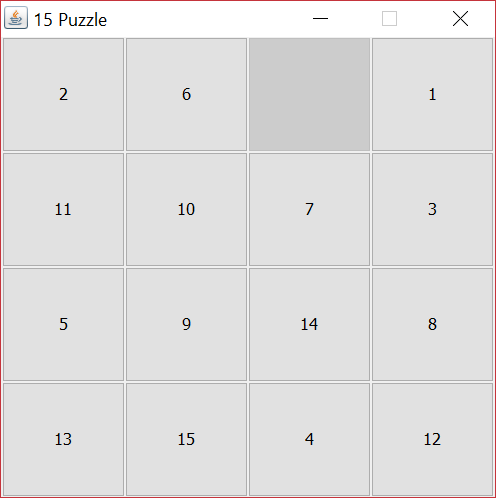
Lab 6 prompted you to create a Swing-based Java GUI for a 15-puzzle, but what if we wanted a program that could solve such a puzzle? It turns out that some puzzles can't be solved, and there is an algorithm that can quickly tell whether a puzzle can or can't be solved.

But what if the puzzle can be solved? How would we solve that problem? The approach we will take is a search algorithm. In this and earlier courses, we have discussed searching through lists or arrays, but this search will look through the space of possible puzzle moves. When you search through a list, all the elements of the list are present. However, the space of all possible puzzle moves is very large, so we will only search through the part of the space, prioritizing moves that look like they're getting us closer to a solution.

Specification

Create a project called Project4, add a package to it called puzzle, and add the following files to that package. Note that Javadoc information is available here.

Both the NumberButton and Puzzle classes have been completed for you. Your only job is to fill in the methods in the Solver and State classes and write JUnit tests in the StateTests class.

State Class

Objects of the State class can hold a snapshot of a Puzzle state. At its heart, objects of this class hold a 2D array of int values corresponding to the button positions in a Puzzle. The only exception is that the empty tile is stored as n2 (16 for a 15-puzzle) instead of as zero. We need this state information for several reasons. First, we will move from State to State, visiting State representations that having lower estimated solution costs, until we (hopefully) reach a State with a cost of zero, meaning that all the tiles are all in the right places. Second, when doing so, we'll keep a set of all of the State representations we've visited, so that we never try a State more than once. Finally, each state will keep a reference to its previous State and the move made from it, allowing us to reconstruct the sequence of moves that reaches a solution.

We're taking things one step at a time here. The State class doesn't actually solve a Puzzle, but it allows us to represent and compare various states the Puzzle might be in, making it easier to solve. A few of the methods are completed for you, but you'll need to complete the following methods in State yourself.

  • State(int[][] state, Puzzle.Direction move, State previous, int blankRow, int blankColumn)
    Constructor called to create a new State object. It sets all of the member variables to the input variables. And it also calls the cost() method and stores the result in the cost member.

  • State getPrevious()
    Accessor to retrieve previous state.

  • Puzzle.Direction getMove()
    Accessor to retrieve move that led to the current state.

  • boolean canMove(Puzzle.Direction direction)
    Method called to determine if moving in a given direction is legal. The direction has a row change and a column change. If the row change added to the row of the blank tile is still a legal row and the column change added to the column of the blank tile is still a legal column, the move is legal; otherwise, the move is not.

  • State move(Puzzle.Direction direction)
    Method called to create a new State object, resulting from moving the blank tile in the direction specified by direction. First, create a new 2D array and copy all of the values from state into it. Next, find the row and the column specified by direction that the blank tile will move to. Then, swap the value in the new array at the current location of the blank tile with the location given by the row and column you just found. Finally, return a new State object built from this 2D array, the specified direction, the current state, and the new row and column for the blank tile.

  • static int cost(int[][] state)
    Static method called to estimate the number of moves needed to solve a state. For each tile (except the blank tile), find the row where it should be (by dividing one less than its value by the width of the puzzle) and the column where it should be (by modding one less than its value by the width of the puzzle). Find the absolute value of the difference between the row where it is and the row where it should be and the absolute value of the difference of the column where it is and the column where it should be and add these values to the total cost. Return this total cost.

    As an example, the cost of the puzzle shown in the picture at the top of the project description has a total cost of 22. You can find this value by summing up all the row and column costs.

    • 2
    Goal: 1
    Row cost: 0
    Column cost: 1    		 6
    Goal: 2
    Row cost: 1
    Column cost: 0    		 Goal: 3 1
    Goal: 4
    Row cost: 0
    Column cost: 3
    11
    Goal: 5
    Row cost: 1
    Column cost: 2    		 10
    Goal: 6
    Row cost: 1
    Column cost: 0    		 7
    Goal: 7
    Row cost: 0
    Column cost: 0    		 3
    Goal: 8
    Row cost: 1
    Column cost: 1
    5
    Goal: 9
    Row cost: 1
    Column cost: 0    		 9
    Goal: 10
    Row cost: 0
    Column cost: 1    		 14
    Goal: 11
    Row cost: 1
    Column cost: 1    		 8
    Goal: 12
    Row cost: 1
    Column cost: 0
    13
    Goal: 13
    Row cost: 0
    Column cost: 0    		 15
    Goal: 14
    Row cost: 0
    Column cost: 1    		 4
    Goal: 15
    Row cost: 3
    Column cost: 1    		 12
    Row cost: 1
    Column cost: 0

  • boolean isSolved()
    Method called to check whether the state is in a solved position. For any tile, if the row times the width of the puzzle plus the column plus one is ever not equal to its tile value, it's not solved. In that case, return false. Once all of the tiles have been checked and none of them violate this rule, the puzzle must be solved, and you can return true.

Solver Class

Now that much of the heavy lifting has been done by the State class, we only need to write a few methods to complete the Solve class. The constructor that sets everything up has been written for you.

  • int[][] initializeState(NumberButton[][] buttons)
    Static method used to create a 2D array of int values corresponding to the values in buttons. First, create a 2D array the same size as buttons. Then, loop through all of the NumberButton objects in buttons and set the corresponding value in the int array to the number from each NumberButton, with one exception: The blank button has number 0 but should be assigned the dimension (width) of the puzzle squared, so that it has the last number.

  • State solve(State startingState)
    Static method that actually finds a solution from a given State. This method explores states in a methodical way, always picking states that haven't been visited and that appear closer to the solution. The method takes the following steps.
    • Create a PriorityQueue of State objects and add startingState to it.. A PriorityQueue lets you store objects ordered by value. In this case, the order is from lowest cost State to highest cost.
    • Create a Set (HashSet is recommended) of visited State objects. This Set records the states we've already visited so that we don't try to visit them twice.
    • As long as the PriorityQueue isn't empty:
      • Remove a State from the PriorityQueue
      • If this State hasn't already been visited:
        • Add the State to the Set of visited states
        • If the State is solved, return it: It's the answer!
        • If the State can move left, add the State that you would get by moving left to the PriorityQueue
        • If the State can move right, add the State that you would get by moving right to the PriorityQueue
        • If the State can move up, add the State that you would get by moving up to the PriorityQueue
        • If the State can move down, add the State that you would get by moving down to the PriorityQueue
    • If you run out of things in the PriorityQueue, it was impossible to find a solution, so return null

Testing

In previous projects, you did not yet know about JUnit tests. Now that you do, we need to write some to test this project. JUnit tests are ideal for unit tests, small tests of the functionality of individual classes and methods. Although professional programmers could (and should) write tests for Solver, you are only required to write the following five tests inside the StateTests class. Note that these tests all test aspects of a State object or the 2D array that represents the data inside of such an object. It's possible to write tests that work on a full 4 × 4 grid, such as we would have for a 15-puzzle. However, it's reasonable to write tests that work on a State that holds only a 2 × 2 or a 3 × 3 grid, since it will be much less work to set up the data.

  • void canMoveSucceedTest()
    Test that constructs an appropriate State object and checks to see if moving in a legal direction is allowed (as it should be).

  • void canMoveFailTest()
    Test that constructs an appropriate State object and checks to see if moving in an illegal direction isn't allowed (as it shouldn't be).

  • void costTest()
    Test that constructs a 2D array of int values that represents the data inside of a State object and checks if the cost estimate is correct. Note that you will have to compute what the cost estimate should be on your own.

  • void isSolvedSucceedTest()
    Test that constructs a State object that is in the solved state (with all the tiles where they go, including the empty tile at the end) and checks to see if it is solved (as it should be).

  • void isSolvedFailTest()
    Test that constructs a State object that is not in the solved state (with at least one tile not in its final position) and checks to see if it is not solved.

Turn In

Your Eclipse project should be called Project4, but the classes you should turn in are Solver, State, and StateTests, all in the package puzzle. Zip up the Solver.java, State.java, and StateTests files from the Project4\src\puzzle folder inside your workspace folder and upload the resulting zip file to Blackboard. Only the team leader should turn in this file. There is no need to include NumberButton.java or Puzzle.java.

All work must be submitted before Friday, April 24, 2020 by 11:59 p.m. unless you are going to use a grace day.

All work must be done within assigned teams. You may discuss general concepts with your classmates, but it is never acceptable for you to look at another team's code. Please refer to the course policies if you have any questions about academic integrity. If you have trouble with the assignment, I am always available for assistance.

Grading

Your grade will be determined by the following categories:

Category Weight
State methods
State constructor 5%
getPrevious() method 5%
getMove() method 5%
canMove() method 5%
move() method 10%
cost() method 10%
isSolved() method 5%
Solver methods
solve() method 20%
initializeState() method 5%
StateTests methods
canMoveSucceedTest() test 5%
canMoveFailTest() test 5%
costTest() test 5%
isSolvedSucceedTest() test 5%
isSolvedFailTest() test 5%
Style and comments 5%

Code that does not compile will automatically score zero points.

Under no circumstances should any member of one group look at the code written by another group. Tools will be used to detect code similarity automatically.