C SC 205 Lecture 13: Trees and Binary Trees
major resources: Data Structures and the Java Collections Framework Second Edition, William Collins, McGraw-Hill, 2005
Introduction to Programming and OO Design using Java, Niño and Hosch, Wiley & Sons, 2002

[ previous | schedule | next ]

Wednesday October 31 (week 8)

Introduction and Trees in General

• So far we have considered only linear collections such as lists. But many collections do not have linear structure. We will consider a hierarchical structure called a tree.
• Here are some examples of tree-shaped structures
• computer file system structure: A file system contains folders. Each folder contains files and other folders, and its folders themselves contain files and other folders. These folders also contain files and yet other folders, etc.
• textbook structure: A book contains chapters. Every chapter contains sections. Every section contains subsections. Every subsection contains paragraphs. Every paragraph contains sentences. Every sentence contains words. Every word contains letters.
• corporate organizational structures: A typical structure has one corporation consisting of several divisions. Each division consists of several departments. Each department has its internal structure.
• corporate personnel structures: One president. Several vice presidents report to president. Several managers report to each vice president. Multiple employees report to each manager.
• Java class hierarchies:All classes (except Object) have one parent class. A class can have multiple child classes.
• A tree is a collection of nodes connected to each other by edges with one node distinguished as the root and in which exactly one path exits from each node to every other node.
• We will skip further tree formalities here and focus on a specialized kind of tree, the binary tree

Introduction to Binary Trees

• Textbook definition: "Binary tree t is either empty or consists of an element, called the root element, and two distinct binary trees called the left subtree and right subtree of t."
• Note this is a recursive definition. Binary trees and recursion go together like (insert favorite analogy here)
• Here is a sample diagram of a binary tree:
  
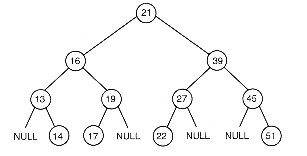
• In this example, each tree element, or node is represented by a circle and its associated value is represented by the number inside the circle
• The root of this tree contains value 21, but every node in this diagram is the root of a subtree.
• Every subtree is itself a binary tree.
• As you can see from the diagram, trees are drawn "upside down" with the root at the top

Binary Tree Terminology

• A node represents each item in the tree.
• A branch (edge) is a line connecting two nodes, and represents a relationship between them.
• A path is the sequence of nodes visited in a traversal of edges from one node to another.
• A leaf is a node whose left and right subtrees are both empty.
• A node's parent is the first node in the path from it to the root. The root has no parents and all other nodes have exactly one parent.
• A node's child is the first node in any path from it to a leaf. A node has either 0, 1 or 2 children.
• All nodes having the same parent are called siblings. Any node in a binary tree can have at most one sibling.
• All elements on the path from a node to the root are ancestors of that node.
• The term descendent is best defined recursively: The descendents of a node consist of its children and all descendents of its children.
• The level (depth) of a node is the number of edges between it and the root.
• The height of a tree is the maximum level of any node.
• A binary tree is full if all leaves are at the bottom level and all non-leaf nodes have exactly two children.
• A full binary tree of height H will have exactly 2^H+1-1 nodes.
• A binary tree is complete if all leaves are at the bottom two levels, and the bottom level leaves are as far "left" as possible. The tree in the diagram above is not complete.
• All full binary trees are also complete, but not vice versa.
• Many of the above terms can be defined recursively. E.g., the ancestor of a node is either its parent or an ancestor of its parent

Binary Tree Specification deferred for now

• We will hold off on specifications until introducing a special kind of binary tree: the binary search tree
• As its name implies, the binary search tree has properties that permit easy binary searches over its elements
• The Java Collections Framework includes neither a BinaryTree nor a BinarySearchTree class or interface.
• The Framework does however include the TreeMap and TreeSet classes implemented using a binary tree. We will cover it later.

A cool array-based implementation for Binary Trees

• Applies equally to binary search trees
• Each array element represents one tree node (element)
• The root is stored in array element 0
• If a node is stored in array element K,
• its left child, if it has one, will be stored in array element 2 * K + 1,
• its right child, if it has one, will be stored in array element 2 * K + 2, and
• its parent, if it has one, will be stored in array element (K - 1) / 2 using integer division.
• If a tree of N nodes is complete or full, it will occupy all array elements from 0 through N-1. No gaps.
• The tree in the diagram above would be represented like this:
  

  [0]

  [1]

  [2]

  [3]

  [4]

  [5]

  [6]

  [7]

  [8]

  [9]

  [10]

  [11]

  [12]

  [13]

  [14]

  [...]

  [n-1]

  21

  16

  39

  13

  19

  27

  45

  14

  17

  22

  51

• Since the tree is neither full nor complete, there are gaps in the array.

A Linked Implementation of a Binary Tree

• Remember the node structure for a linked list? Each node in a singly-linked list had two components: the element reference and a link to the next node in the list. A doubly-linked list added a second link to the previous node.
• The node structure for a binary tree requires the element reference and at least two links: to the left child and the right child.
• You may also add a third link: to the parent. This is equivalent to the previous link in a doubly-linked list. Convenient but not absolutely necessary.
• We can visualize like this:
  
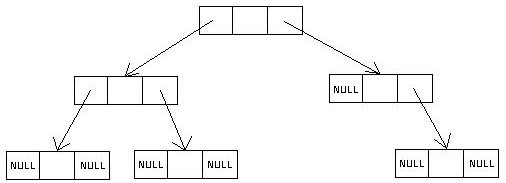
• In this diagram, the parent link is not used and the element values (middle box) are not shown.

Traversing a Binary Tree

• Lists allow only one linear traversal, from beginning to end (or back, using recursion or doubly-linked implementation). There are several different techniques for traversing a binary tree. We will look at the most useful ones.
• pre-order traversal
• in-order traversal
• post-order traversal
• A tree traversal starts with the root and is completed when every node has been visited exactly once. The techniques listed above refer to the order in which nodes will be visited.
• Consider a tree or subtree consisting of three nodes: a root and its two children. Call them A, B, and C.
  
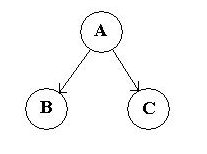
• In a pre-order traversal, these three nodes would be visited in the order: A then B then C. In other words, the parent is visited before its children. Parent, then left child, then right child.
• In an in-order traversal, these three nodes would be visited in the order: B then A then C. In other words, the parent is visited between its children. Left child, then parent, then right child.
• In a post-order traversal, these three nodes would be visited in the order: B then C then A. In other words, the parent is visited after its children. Left child, then right child, then parent.
• Real trees are more complex than this, so we need a more precise yet general definition for traversal. Here are possible definitions for the three traversals. These definitions would appear either as methods or incorporated into methods of a binary tree class. They use a little inner class called BTEntry that has three fields: leftChild, rightChild, and element. The first two are references to other BTEntry objects and the third holds the element value.
  
  

  // THESE ARE NOT NECESSARILY METHODS OF A BinaryTree CLASS. protected void preOrder(BTEntry<E> node) { if (node != null) { visit(node); preOrder(node.leftChild); preOrder(node.rightChild); } } protected void inOrder(BTEntry<E> node) { if (node != null) { inOrder(node.leftChild); visit(node); inOrder(node.rightChild); } } protected void postOrder(BTEntry<E> node) { if (node != null) { postOrder(node.leftChild); postOrder(node.rightChild); visit(node); } } protected void visit(BTEntry<E> node) { // do any processing here, such as System.out.println(node.element); }

  
  
• Notice anything interesting?Yes, the traversals are all recursive! The code is very simple, yet each will completely traverse an arbitrarily-shaped binary tree in its particular order.
• The pre-order traversal is also known as a Depth First Search. The traversal goes as deep to the left as possible before proceeding to the right.
• The above traversals can also be accomplished using a non-recursive method in conjunction with an auxiliary Stack to hold nodes waiting to be processed. Recursion provides stacking automatically through the system's stack frames.
• A Breadth First Search will traverse the tree starting at the root and visiting each level completely from left to right order before dropping to the next level.
• The breadth first traversal is easily accomplished using a non-recursive method that employs a Queue for auxiliary storage. See textbook definition pages 382-383.

Binary Tree Example: arithmetic expressions

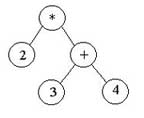
This tree represents the expression "2 * (3 + 4)". Notice that the tree did not need to store parentheses -- the right child of the "*", which is the result of the "+", has to be evaluated before the "*" can be evaluated.

Notice this also: Suppose you perform a pre-order traversal of this tree and print the value stored at each visited node. What is the output? Suppose you do the same thing with a post-order traversal?