C SC 205 Lecture 12: Stacks and Queues
major resources: Data Structures and the Java Collections Framework Second Edition, William Collins, McGraw-Hill, 2005
Introduction to Programming and OO Design using Java, Niño and Hosch, Wiley & Sons, 2002

[ previous | schedule | next ]

Monday October 29 (week 8)

The Stack concept and example specifications

• Stack: linear collection in which elements may be added and removed only from one end designated as the "top"
• Textbook defines the interface PureStack
• int size()
• boolean isEmpty()
• void push(E element)   (add an element to the collection)
• E pop()   (remove an element from the collection)
• E peek()   (access top element without removing it)
• Time complexity for push() is linear in the worst case but constant on average; the others are constant all the way
• This interface is not part of Java Collections Framework (we'll see why later)

Consider possible implementations of PureStack

1. An array implementation
• Major data structure is array of E
• Where is the "top" and where is the "bottom"? (note time complexity specs)
• Since array sizes are fixed at creation, need ability to grow it
• When creating array of E, need to say (E[]) new Object[capacity]; (new cannot be used with parameter type)
2. A linked list implementation
• Consider extending SinglyLinkedList? Why or why not?
• Consider using SinglyLinkedList as data structure? Why or why not? Consider time complexities
• Consider using LinkedList as data structure? Why or why not?
• Textbook shows source code for using a singly linked list written from scratch
• Note that push() time complexity is (or should be) constant in the worst case
3. The java.util.Stack class extends java.util.Vector
• Both are members of the Java Collections framework
• The Vector class is similar to, but older than, ArrayList
• Resulting time complexities are same as for array implementation above
• Why is-a Vector instead of has-a? Good question
• A Stack object inherits and thus makes available to its clients all the public Vector methods (Vector implements Collection and List so there are a lot)

Stack applications

• There are innumerable applications. Textbook details a couple:
• Stack frames (execution frames, activation records) to represent each activation of a method at runtime
• Converting infix (e.g. a + b) expressions to postfix (e.g. a b +) -- we'll explore this in a Lab project

The Queue concept and example specifications

• Queue: linear collection in which elements may be added only at one end designated as the "back" and removed only from the other end designated as the "front"
• Textbook defines the interface PureQueue
• int size()
• boolean isEmpty()
• void enqueue(E element)   (add an element to the collection)
• E dequeue()   (remove an element from the collection)
• E front()   (access front element without removing it)
• Time complexity for enqueue() is linear in the worst case but constant on average; the others are constant all the way
• This interface is not part of Java Collections Framework
• The analogy to PureStack methods is obvious

Consider possible implementations of PureQueue

1. An array implementation
• I think we agree that extending the ArrayList class is not the right approach
• Consider using ArrayList as data structure? Why or why not? Consider time complexities
• Major data structure is array of E
• Where is the "front" and where is the "back"? (note time complexity specs)
• Since array sizes are fixed at creation, need ability to grow it
• What is the major implementation issue here?
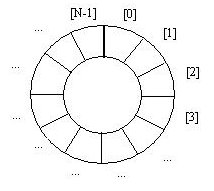
• Consider a home grown "circular array"
• Suppose array of N elements with Front pointer initially 0 and Back pointer initially -1
• Enqueue: increment back pointer, then add element at back pointer position
• Dequeue: remove element from front pointer position, then increment front pointer
• Both increments are "mod N", so if at position N-1, wraps around to array element 0!
• If the queue has exactly one element, both pointers have same value
• What happens if queue has one element and dequeue occurs?
• Yes, if the queue is "empty", back pointer is at front-1 mod N
• But wait, if the queue is "full", back pointer is also at front-1 mod N
• Maintain size variable to distinguish full from empty
• If the queue is "full" and enqueue occurs, need to expand the array
• Does this implementation meet specification's time complexity requirements?

2. A linked list implementation
• I think we agree that extending a linked list class is not the right approach
• Consider using SinglyLinkedList as data structure? Why or why not? Consider time complexities
• Consider using LinkedList as data structure? Why or why not?
• Textbook shows source code for using a LinkedList backing data structure
• data structure: LinkedList<E> list;
• Method definitions based on that data structure:
• constructor: list = new LinkedList<E>();
• size: return list.size();
• isEmpty: return list.isEmpty();
• enqueue: list.addLast(element);
• dequeue: return list.removeFirst();
• front: return list.getFirst();
• What do you notice about method implementations?
• This is a technique known as delegation. The responsibilities of the queue class are delegated to the methods of a different class via an instance variable.
3. Implementing java.util.Queue interface
• Java Collections framework includes a Queue interface
• However it extends the Collection interface!
• This means an implementing subclass is obliged to implement all the Collection methods, many of which exhibit "non-queue-like" behaviors
• Yes, we can implement them to throw UnsupportedOperationException, but still...
• There's also the matter of Queue methods:
  • offer() to enqueue,
  • poll() or remove() to dequeue
  • peek() or element() to access front element without removing
• Even the method names are not queue-like!
• On the other hand, queue variations are widely used.
• One common variation is the priority queue, in which the queue is ordered based on an element's value

Queue applications

• Again, there are a myriad of applications for queues
• Operating System buffers are an example
• Queues are essential for computer simulation modeling
• Don't let me get started on the topic of simulation programming!

Queueing theory

• Wikipedia definition: "The mathematical study of waiting in lines"
• Also spelled "queuing" instead of "queueing"
• Entities wait in line to be served
• Our concern is in the balance of arrivals and service
• Here's a basic introduction
• Assume a single server and single queue
• Characterize arrivals into the queue
• Arrival rates (arrivals per period of time) have Poisson distribution, assume mean of λ (lambda).
• Interarrival times are the inverse: exponential distribution, mean of 1/λ.
• Characterize service, which determines departures from the queue
• Service rates (number of entities served per period of time) also have Poisson distribution, assume mean of μ (mu).
• Service times are the inverse: exponential distribution, mean of 1/μ.
• NOTE: The assumption of Poisson distribution for service rates is not realistic -- arrivals are truly random but service is not -- but it is close and is required to keep the math simple
• Must assume λ < μ; otherwise system is out of balance (arrivals faster than service)
• Given those definitions, we can easily estimate average system performance measures
• Average Queue Length: (λ * λ) / (μ * (μ - λ))
• Average Time in Queue: λ / (μ * (μ - λ))
• Average Time in System: 1 / (μ - λ)
• Server Utilization: λ / μ
• There are equations for multiple server systems but they are more complex
• Example: Car Wash
• Customers arrive every 6 minutes (10 customers per hour)
• Wash takes 5 minutes (services 12 customers per hour)
• λ = 10,   μ = 12
• Average Queue Length: 4.17 = (10 * 10) / (12 * (12 - 10))
• Average Time in Queue: 25 minutes = .417 hours = 10 / (12 * (12 - 10))
• Average Time in System: 30 minutes = .5 hours = 1 / (12 - 10)
• Server Utilization: 83% = .833 = 10 / 12
• Were customers to arrive in "lockstep", e.g. every 6 minutes, there would be no waiting! But utilization would be the same...huh?
• But customers arrive randomly...we've all experienced this phenomenon.