COMP 3400 Lecture 6: Process Synchronization
[ previous
| schedule
| next ]
additional resource: Modern Operating Systems (2nd Ed), Tanenbaum,
Prentice Hall, 2001.
Note: All the problems, solutions, and algorithms in this lecture apply equally
to both processes and threads.
The synchronization problem
Illustrated with print spooler problem
A print spooler is software that permits "background" printing. Since printers
are slower than just about everything, a user should be able to submit a print request, then
continue working. The term spooler is fron the acronym SPOOL: Simultaneous
Peripheral Operations On-Line.
Suppose the print spooler uses a circular queue of file names as its data structure.
The queue has front and rear indexes (to indicate the first and
last file names in the queue. These data structures are shared by all
processes that call the spooler's addToPrintQueue() method - a partial version is shown here:
void addToPrintQueue(String fileName) {
int nextSlot = (rear+1) % queue.length;
queue[nextSlot] = fileName;
rear = nextSlot;
}
Files are removed from the queue by another process called the print daemon.
We will not consider the print daemon here.
Example run 1: beginning configuration of spooler's shared memory
is this
| front |
rear |
queue |
| | [0] | [1] |
[2] | [3] | [4] |
| 0 |
2 |
myfile.txt |
silly.java |
resume.doc |
|
|
Sequence of operations -- number in parentheses indicates sequence 1-6.
| Process 1 (fileName is osh.c) | Process 2 (fileName is index.html) |
void addToPrintQueue(String fileName) {
(1) int nextSlot = (rear+1) % queue.length;
(2) queue[nextSlot] = fileName;
(3) rear = nextSlot;
}
|
void addToPrintQueue(String fileName) {
(4) int nextSlot = (rear+1) % queue.length;
(5) queue[nextSlot] = fileName;
(6) rear = nextSlot;
}
|
Analysis: everything is OK. After both processes are finished, the shared
data structure looks like this:
| front |
rear |
queue |
| | [0] | [1] |
[2] | [3] | [4] |
| 0 |
4 |
myfile.txt |
silly.java |
resume.doc |
osh.c |
index.html |
Example run 2: beginning configuration of shared memory is same as before
| front |
rear |
queue |
| | [0] | [1] |
[2] | [3] | [4] |
| 0 |
2 |
myfile.txt |
silly.java |
resume.doc |
|
|
Sequence of operations -- number in parentheses indicates sequence 1-6.
| Process 1 (fileName is osh.c) | Process 2 (fileName is index.html) |
void addToPrintQueue(String fileName) {
(1) int nextSlot = (rear+1) % queue.length;
(5) queue[nextSlot] = fileName;
(6) rear = nextSlot;
}
|
void addToPrintQueue(String fileName) {
(2) int nextSlot = (rear+1) % queue.length;
(3) queue[nextSlot] = fileName;
(4) rear = nextSlot;
}
|
Analysis: everything is not OK! What happened? After both processes are finished, the shared
data structure looks like this:
| front |
rear |
queue |
| | [0] | [1] |
[2] | [3] | [4] |
| 0 |
3 |
myfile.txt |
silly.java |
resume.doc |
osh.c |
|
Moral of the story:
When the outcome of an execution differs depending on the particular sequence in which
usage of the shared variable occurs, we call the situation a race condition.
Opportunities for these abound in software design (especially database design), and in OS design itself since
several OS processes often work concurrently on the same kernel data structure.
Critical Section
Program segments where shared data are used by processes/threads are called critical
sections.
This is a section of code that no two threads can concurrently execute;
each must have mutually exclusive use of the shared variable.
Illustrated with producer-consumer problem
For a more subtle example, let's look at the producer-consumer problem.
- AKA the Bounded Buffer
- Buffer holds data, Producer adds data to the buffer, Consumer removes data from the buffer
- Producer and Consumer cooperate through shared memory or message passing
- See naive BoundedBuffer class below (not a good solution; we'll see why)
- Note: if we wrote an equivalent C program using fork() to create the producer
and consumer, the solution would have to be written differently because producer and consumer would be different processes
and have no shared memory. They can of course communicate through pipes or files as
in the example we studied earlier.
Here is a naive implementation of a BoundedBuffer class
public class BoundedBuffer implements Buffer {
private static final int BUFFER_SIZE = 3;
private int count;
private int in; // points to the next free position in the buffer
private in out; // points to the next full position in the buffer
// Constructor is omitted; it initializes in and out, creates buffer
// Called only by producer
public void insert(Object item) {
while (count == BUFFER_SIZE)
; // do nothing
++count;
buffer[in] = item;
in = (in + 1) % BUFFER_SIZE;
}
// Called only by consumer
public Object remove() {
while (count == 0)
; // do nothing
--count;
Object item = buffer[out];
out = (out + 1) % BUFFER_SIZE;
return item;
}
}
Now, focus on manipulation of the shared variable count, in the insert() statement
++count; and the remove() statement --count;.
In a compiled language like C or C++, the statement ++count; would be compiled
into an assembly language statement sequence something like this:
LOAD $1, count
ADD $1, 1
STORE $1, count
($1 is general purpose register 1).
Similarly, --count; would be compiled into something like:
LOAD $1, count
SUBTRACT $1, 1
STORE $1, count
Consider this execution scenario:
- The current value of count is 2. There are 2 items in the buffer.
- The producer is running and the consumer is next in the ready queue.
- The producer produces a new item and calls insert().
- The producer executes code to place the item into the buffer.
- The producer executes: LOAD $1, count (loads 2 into register)
- The producer executes: ADD $1, 1 (increments register value to 3)
- A higher priority thread interrupts and producer is preempted.
- The interrupting process/thread completes and scheduler selects consumer to run.
- The consumer calls remove()
- The consumer executes: LOAD $1, count (loads 2 into register)
- The consumer executes: SUBTRACT $1, 1 (decrements register value to 1)
- The consumer executes: STORE $1, count (stores 1 into count)
- A higher priority thread interrupts and consumer is preempted.
- The interrupting process/thread completes and scheduler selects producer to run.
- The producer executes: STORE $1, size (stores 3 into count)
- The producer is finished with insert()
- The scheduler selects consumer to run.
- The consumer copies the item from the buffer and finishes with remove()
- The producer calls insert() with another item but spins in the while loop
because it thinks the buffer is full (count is 3 but should be 2).
There are many other scenarios that lead to such errors, and many that work perfectly
well.
Mutual exclusion (mutex) solutions
We'll look at several possible means of assuring a process/thread mutually exclusive access
to its critical section. A good solution must meet these criteria:
- mutual exclusion: no more than one process can be executing its critical section at a time
- progress: a process not in its critical section cannot block another process from entering its own
critical section
- finite wait: no process should be allowed to starve, e.g. have to wait indefinitely to enter
its critical region
- relative speed: the above three criteria must be met regardless of the number or speeds of CPUs involved
In the sections to follow, we will describe and evaluate several possible solutions
to the mutual exclusion problem. They include:
- disabling interrupts
- Peterson's solution
- Test-and-Set-Lock machine instruction
- semaphores
- monitors
Disabling Interrupts
One way to assure that a process can not be interrupted while in its critical section is
to disable system interrupts upon entry and re-enable them upon exit. This is appealing in
its simplicity but is not viable because it gives user processes too much power -- suppose
the critical section gets caught in an infinite loop?
An effect similar to this is achieved through nonpreemptive kernels. This
is where a process cannot be preempted while running in kernel mode. Windows XP does this, as
did Linux until kernel version 2.6.
Peterson's Solution
Assures mutual exclusion between two processes, but does not work for more than two.
Define a shared int (or boolean) variable called turn, initialized to either 0 or 1.
This keeps track of whose turn it is to enter the critical section. A process awaits its turn
using the technique of busy waiting -- in a continous loop testing turn value.
Define a shared data structure: a boolean array
called, say, ready, with two elements (one per process). ready[i] indicates whether or not
process i is ready to enter its critical section.
/* Process i code. Assume j (1-i) is the other process */
while (true) {
ready[i] = true;
turn = j;
while (ready[j] && turn == j)
;
criticalSection();
ready[i] = false;
nonCritical();
}
This works in the crucial scenario that both processes attempt to enter their
critical section at about the same time: each sets turn to the other's ID but only
the second such assignment will "stick"; the first is overwritten. Thus turn will
have the ID of the first one! Think about it...
Consider the while condition from its inverse: process i will spin in the while
loop until either it is i's turn or j is not ready
(e.g. j is in its nonCritical section).
Briefly addressing the criteria for critical sections:
Mutual exclusion: Since turn is not modified
inside the critical section and turn cannot simultaneously have the
values i and j, the turn==j condition alone would insure mutually
exclusive access to the critical section (in strict alternation).
Progress: The ready array is needed
to assure the progress requirement. In other words, process i should be able
to enter its critical section if it is ready and process j is not ready,
regardless of whose turn it is. The ready[j] term in the while condition assures this.
Starvation:If i is in the critical section and j wants to be, then j is assured
of getting in the critical section before i can have it again. Explanation: In this situation, j is spinning
in its while loop having set ready[j] = true;. In the worst case, i will continue to run after finishing its critical section
then perform its non-critical section and become ready to use its critical section again. Just before
its while loop, i will set turn = j;. Then i will
begin spinning in its while loop, because j is ready and it is j's turn. Eventually, j gets to run again
and in the next spin of its while loop the condition will be false because it is j's turn. Then j
can enter its critical section.
Nice solution but it only works for two processes plus it uses busy-waiting, a nuisance and CPU-time-waster that we'll deal with later.
Test-and-Set-Lock machine instruction
This solution requires the hardware to have a machine instruction TSL
(Test-and-Set-Lock). This machine instruction has the format:
TSL RX, LOCK
where RX is a machine register and LOCK is a shared variable. What the
instruction does is loads the value of LOCK into register RX then sets
the value of LOCK to 1, indivisibly! Since it is a single machine instruction
it cannot be interrupted partway through. If the two operations could be separated, it would
not work reliably.
The shared variable acts as a lock:
- If a process sees the lock is 1, it cannot
enter its critical section.
- If a process sees the lock is 0, it sets the lock to 1, then enters and runs its critical
section and then resets the lock to 0 afterward.
Thus a process wanting to enter its critical section follows this sequence (pseudo assembly code):
TRY: TSL REGISTER, LOCK # copy lock value into register and set LOCK to 1.
CMP REGISTER, ZERO # compare value in register to 0.
BNE TRY # if not equal to 0, loop back to try again
# Critical section goes here
MOV LOCK, ZERO # sets LOCK to 0
# Non-critical section goes here
B TRY # go back jack and do it again
Note that if LOCK was initially 1, the TSL just sets it to its same value.
Expressing it in Java
class Lock {
private boolean lockVar = false;
public boolean get() { return lockVar; }
public void set(boolean val) { lockVar = val; }
}
// This is an indivisible operation
boolean testAndSet(Lock lok) {
boolean result = lok.get();
lok.set(true);
return result;
}
// code that uses shared Lock variable lock
while (true) {
while (testAndSet(lock))
;
criticalSection();
lock.set(false);
nonCritical();
}
Fast solution, fast, works for any number of processes, but starvation
is possible and it uses busy-waiting and requires machine support. It is also
complicated to use.
The starvation issue can be addressed using, in addition to the lock, a boolean
array with one element per process. The array element indicates whether or not
the process is waiting for the lock. This does not affect the TestAndSet()
operation but makes the client code for obtaining and releasing the lock even
more complex.
Semaphores
This technique for mutual exclusion was developed in the 1960's by Edsgar Dijkstra
(who passed away in summer 2002). A semaphore is an shared variable that,
once initialized, can be accessed only through operations called P() and V().
These are acronyms for Dutch words, so most call them by different names:
P() is also known as acquire() or down()
and V() is also known as release() or up().
We will use acquire() and release() terminology.
Semaphores come in two flavors: binary and counting. The former is used
to assure mutual exclusion, the latter to permit up to a given fixed number of processes
into a code section simultaneously.
The basic usage of a binary semaphore is as follows:
- the semaphore is created and initialized before any process attempts its critical section
- a process wishing to access its critical section calls acquire().
- after the return from acquire(), the process enters its critical section.
- after completing its critical section, the process calls release().
Client usage is stated more succinctly as :
Semaphore mutex; // shared among all processes
. . .
while (true) {
mutex.acquire();
criticalSection();
mutex.release();
nonCritical();
}
A newly-created semaphore is normally initialized to the maximum number of processes which
should be simultaneously allowed into the code it protects. For binary semaphore, this is 1.
A semaphore can be used to coordinate any number of processes, and semaphores
do not use busy-waiting. In order for semphores to work, the acquire()
and release() operations must be indivisible.
The components of a semaphore could be expressed using Java class notation:
public class Semaphore {
private int value;
private PCBList blockList;
public Semaphore(int init) {
value = init;
blockList = new PCBList();
}
// JAVA-LIKE IMPLEMENTATIONS OF acquire() AND release() DISPLAYED SIDE-BY-SIDE
//
public void acquire() { public void release() {
value--; value++;
if (value < 0) { if (value <= 0) {
blockList.add(thisProcess); process p = blockList.remove();
thisProcess.block(); p.wakeup();
} }
} }
}
In acquire(), variable thisProcess refers to the currently running process.
Assume PCBList is a collection structure for holding a list of Process Control Blocks.
The normal operation of a binary semaphore is as follows:
- The semaphore, call it mutex, is created and initialized to 1.
- Process A reaches its critical section, calls mutex.acquire()
- The semaphore value is decremented to 0, the if condition fails, and acquire() returns.
- Process A goes into its critical section.
- Process B reaches its critical section, calls mutex.acquire()
- The semaphore value is decremented to -1, the if condition is true, and process B blocks.
- Process A emerges from its critical section, calls mutex.release()
- The semaphore value is incremented to 0, the if condition is true, and process B is awoken.
- The next time process B runs, it resumes, returns from mutex.acquire()
- Process B goes into its critical section.
- etc.
Remember I stated that a semaphore can coordinate any number of processes? Check out this
sequence:
- The semaphore, call it mutex, is created and initialized to 1.
- Process A reaches its critical section, calls mutex.acquire()
- The semaphore value is decremented to 0, the if condition fails, and acquire() returns.
- Process A goes into its critical section.
- Process B reaches its critical section, calls mutex.acquire()
- The semaphore value is decremented to -1, the if condition is true, and process B blocks.
- Process C reaches its critical section, calls mutex.acquire()
- The semaphore value is decremented to -2, the if condition is true, and process C blocks.
- Process D reaches its critical section, calls mutex.acquire()
- The semaphore value is decremented to -3, the if condition is true, and process D blocks.
- Process A emerges from its critical section, calls mutex.release()
- The semaphore value is incremented to -2, the if condition is true, and one of processes B, C or D is awoken.
- etc.
Two things to note about this second sequence:
- When mutex.release() is called and has a negative value, the absolute value
represents the number of processes blocked on this semaphore.
- When mutex.release() is called and there is more than one blocked process in the list,
the semaphore specification does not address which process is selected for awakening.
The discussion below on classical problems includes a producer-consumer solution that uses
both a binary semaphore and two counting semaphores. The counting semaphores are used to
maintain the empty/full status of the buffer.
Semaphores meet all the criteria for good mutual exclusion.
Monitors
The knock against semaphores is they are primitive and unstructured, and have to be
used very carefully. A single misplaced call to acquire() or release(), particularly
when more than one semaphore is in use (see producer-consumer solution below), results
in erroneous operation or complete deadlock!
In the 1970s, Tony Hoare and Per Brinch Hansen developed a structured synchronization
mechanism called monitors.
A monitor is a language structure that resembles a class. It is a module that
consists of variables, procedures and special constructs called conditions.
It is tightly encapsulated: procedures may access only their local variables,
monitor variables and conditions; monitor clients may access only its procedures.
Every procedure defined in a monitor inherently defines a critical section.
In other words, only one process can be active in a monitor at a given instant.
Here is an outlined pseudocode example (keywords in bold):
monitor BoundBuffer {
int i;
condition x, y;
procedure insert() {
. . .
}
procedure remove() {
. . .
}
BoundBuffer() {
. . .
}
}
Every condition variable has two associated operations, wait()
and signal().
- When a condition's wait() is called, the process
making the call is blocked.
- When this occurs, the process is considered to no longer be "in the
monitor" so another process waiting for the monitor can enter.
- When a condition's signal() is called, a process
blocked on that condition, if any, is awakened (scheduled to run).
- If there was no process to awaken, nothing happens and the caller continues running.
- If a process is awakened, the process issuing the
signal() is required to immediately exit the monitor; otherwise both it and
the newly-awakened process would both be in the monitor -- this violates mutual exclusion.
Classical synchronization problems
We'll look briefly at a few:
- Bounded buffer producer-consumer (two versions)
- Readers-writers
- Dining philosophers (apologies to A. Mill)
Bounded Buffer producer-consumer with monitors
As an example, the bounded (blocking) producer-consumer could be implemented
using two condition variables, one for a full buffer and another for an empty
buffer. Insert and remove could be implemented as monitor procedures something
like this:
monitor BoundBuffer {
final int CAPACITY;
Buffer buffer;
condition empty, full;
BoundBuffer(int capacity) {
CAPACITY = capacity;
buffer = new Buffer(CAPACITY);
}
// PROCEDURES ARE PLACED SIDE BY SIDE FOR DISPLAY PURPOSES
//
// called only by producer. // called only by comsumer.
procedure insert(Object item) { Object procedure remove() {
if (buffer.size()==CAPACITY) { if (buffer.size()==0) {
full.wait(); empty.wait();
} }
buffer.add(item); Object item = buffer.remove();
if (buffer.size()==1) { if (buffer.size() == CAPACITY-1) {
empty.signal(); full.signal();
} }
} return item;
}
} // end of monitor
Bounded Buffer producer-consumer with semaphores
You are familiar with the problem as well as a couple solutions. Here I
present the essential parts of a blocking solution that uses semaphores:
// Create semaphores in a place global to both producer and consumer...
Semaphore mutex = new Semaphore(1);
Semaphore empty = new Semaphore(CAPACITY);
Semaphore full = new Semaphore(0);
Buffer buffer = new Buffer(CAPACITY);
mutex initial value is the number of processes/threads allowed in the critical section
simultaneously. empty initial value is the number of empty buffer slots.
full initial value is the number of filled buffer slots.
// Called only by producer. // Called only by consumer.
public void insert(Object item) { public Object remove() {
empty.acquire(); full.acquire();
mutex.acquire(); mutex.acquire();
buffer.add(item); Object item = buffer.remove();
mutex.release(); mutex.release();
full.release(); empty.release();
} return item;
}
Note: the producer call to empty.acquire(); will block the producer if the buffer is full! Study
the initial value of empty and the code for acquire() to convince yourself of this.
Its subsequent call to full.release() will awaken a consumer blocked for an empty buffer, if any.
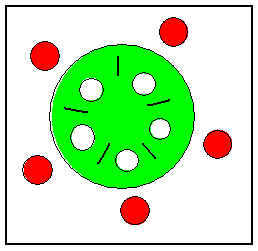
Dining Philosophers with semphores
- Five philosophers sit at a round table.
- Each has a
plate full of noodles in front of her and one chopstick on either side of her.
- There are
thus five plates and five chopsticks (one person's left chopstick is also her left
neighbor's right chopstick).
- A given philosopher alternates between
thinking and eating.
- To eat, a philosopher has to pick
up the two chopsticks on either side of her.
- She can pick up only one at a time, and cannot pick up a chopstick being used by her neighbor.
- Once in possession of both chopsticks, she eats until satisfied then relinquishes them and goes back to thinking.
- What is the largest number of philosophers who can eat simultaneously?
|
 |
Obviously, a chopstick is the resource requiring mutually exclusive access.
It is overly restrictive to assign one semaphore to represent all the chopsticks -- this
allows only one philosopher to eat at a time. Suppose you define a semaphore for each chopstick.
One possible solution is:
while (true) {
chopStick[left].acquire();
chopStick[right].acquire();
eat();
chopStick[left].release();
chopStick[right].release();
think();
}
Surprisingly, this solution is not guaranteed to work! Suppose all five philosophers
decide to eat at about the same time and all are able to get their left chopstick
before any can get their right chopstick?!? What happens?
This can be solved using semaphores, and the textbook shows a solution using
monitors. Both solutions are a somewhat complex and will not be considered here.
They involve recording each philosopher's state: thinking, hungry, or eating.
This introduces the "hungry" state to describe the period between
wanting to eat and having control of both chopsticks.
Dining Philosophers with monitors
See solution in textbook. As with the semaphore solution, it
requires each philosopher to be in one of three states: thinking, hungry, or eating.
While thinking, the philosopher is not interested in eating. While hungry, the
philosopher wants to eat but does not yet have control of both chopsticks. Once
both are obtained, the philosopher transitions to the eating state and when finished
relinquishes both chopsticks.
There is a nice applet that animates and traces the progress of a 5 person Dining Philosopher
problem. See http://users.rcn.com/ziring/diningAppletDemo.html
Readers and Writers
A classic database problem involves maximizing the safe usage of a database by multiple
concurrent processes. Processes are grouped into two categories:
- readers are processes which wish only to read from the database.
- writers are processes which wish to both read and write (update) the database.
If all the processes are "readers", there is no need for mutually exclusive access; all
can read concurrently without problem. Any "writers", however, must have mutually
exclusive access to the database. A general solution must assume the process mix includes both
readers and writers.
We will not cover solutions in detail. One solution strategy is this:
- a writer simply gets mutex on database, does its thing, then relinquishes.
- The reader strategy is more complex, but allows multiple readers to be active in
the database at the same time. This requires a shared variable that counts
the number of readers currently using the database. A reader increments the count
then checks its value. If count is 1 (no reader currently active), it has to get
mutex on database before using. Otherwise, it can go ahead and use the
database at will. Any reader has to decrement the reader count when finished using
the database. A reader who decrements it to zero has to relinguish mutex on the database.
- What happens if readers consistently come along more frequently than writers?
An alternate solution does not permit new readers into the database while a writer is
waiting. What happens if writers consistently come along more frequently than readers?
The weakness in both solutions is they give one category of processes priority
over the other and starvation can occur. There are better solutions.
Synchronization in Java
Java provides some language support for implementing mutual exclusion. Here is
the lowdown:
- The mutex mechanism is a simplied version of a monitor.
- Every Java object has an associated lock. Sun's Java API documentation
refers to this lock as the object's monitor.
- A method can be declared a critical section using the synchronized keyword. It
goes right before the return type, e.g. public synchronized Object remove() { . . }
- To use the critical section, the client need only call the method!
- JVM checks the lock associated with the object through which the call
was made.
- If object not locked, JVM locks it for this thread and the thread gains entry to the method.
- If object already locked, JVM blocks the calling thread, placing it in the lock's entry set.
- When a thread leaves a synchronized method, the lock is released. JVM checks its entry set.
- If entry set not empty, JVM arbitrarily selects one blocked thread and
and locks the object for it.
- Every Java object also has a single unnamed condition variable associated with it.
- It has a wait set of threads waiting on the condition variable
- A thread joins the wait set by calling the wait() method
- A thread is removed from the wait set when another thread calls the notify() or notifyAll() method (if wait set is empty, nothing happens)
- wait() and notify() are analogous to the monitor condition wait and signal operations
- The thread calling wait() becomes blocked and loses its lock. This allows another thread to enter
its critical section.
- A thread being removed from wait set becomes runnable and is placed in the lock's entry set.
- wait(), notify() and notifyAll() are methods of the Object class
thus all objects inherit them.
- A variable can be declared volatile. This is useful for variables shared between threads. Basically, this
means every time the variable's value is changed, the new value is written immediately to main memory. If the volatile keyword
is not used, the compiler may decide to keep the variable's value in a register for awhile. Since each thread has its own
register set, this can cause problems in a multithreaded environment.
- Java does not provide semaphores natively, but they are available in a couple ways:
- A Semaphore
class was added with Java 1.5 (5.0) as part of the
java.util.concurrent package
- Before Java 1.5, homegrown semaphores were implemented using synchronized, wait(), and notify().
Additional notes:
If only a portion of a method needs to be a critical section,
it
can
instead
be placed in front of a code block, e.g. synchronized(this) { . . }
I have read that use of volatile can in limited cases substitute for small critical sections. For example:
public class VolDemo {
private volatile count = 0;
public void yin() {
count++;
}
public void yang() {
count--;
}
}
In this example, the operations count++ and count-- are done atomically (indivisibly)
because
count is declared volatile. If the critical section were to
consist only of that statement, then
synchronized is not needed. My information resource for this tidbit
is
http://www.javaperformancetuning.com/tips/volatile.shtml
New in Java 1.5 (5.0)
The Java API now includes the
java.util.concurrent package, which provides a number of handy interfaces and classes to
support concurrent programming.
Those most relevant to our concurrency coverage are:
-
Semaphore class to provide counting semaphores. Recall a binary semaphore is just a counting
semaphore initialized to 1.
-
ArrayBlockingQueue class to provide a bounded FIFO queue (bounded buffer) implemented using
an array, with blocking as appropriate when queue is empty or full.
-
LinkedBlockingQueueclass to provide a bounded or unbounded FIFO queue (bounded buffer) implemented using
a linked list, with blocking as appropriate.
[ COMP 3400
| Peter Sanderson
| Math Sciences home page
| Otterbein
]
Last updated:
Peter Sanderson (PSanderson@otterbein.edu)
