CSC 150 Chapter 11: Models of Computation
primary information resource:
An Invitation to Computer Science (Java), Third Edition,
G. Michael Schneider and Judith L. Gersting,
Course Technology, 2007.
[ previous
| schedule
| next ]
What is a model?
Why study Models of Computation?
One such model is the Turing Machine
-
Developed in 1935-36 by mathematician Alan Turing
-
brief Turing bio
-
Hilberts 3rd question: is mathematics decidable?
-
abstracts and extends typewriter
Turing machine consists of the following components:
-
An infinite storage “tape” partitioned into cells
-
An alphabet of symbols
-
A read/write head
-
The machine state
-
A set of instructions (program), stored in a 2D table or set of tuples
Instruction format is:
(current state, current symbol, next
symbol,
next state, direction)
The TM interprets instruction (i, j,
k,
s,
d)
as:
IF current state
is
i
AND current symbol is j
THEN
Write
symbol k on tape (replacing j)
Set machine
state to s
Move read/write
head one cell in direction d
ENDIF
Additional TM Rules:
1.
finite number of symbols on the tape (blanks on both sides).
2.
initial configuration of TM is:
-
finite input contained on tape
-
the R/W head is positioned at the first (leftmost) input symbol,
-
initial state is specified (usually 0 or 1).
3.
If no instruction for current state and input symbol exists, the machine
halts.
4.
The output is what remains on the tape when the machine halts
Behold the power!
Any
computable function can be computed with a TM!
TM has same algorithmic power as Java or any other high
level language!
Church-Turing
thesis (not proved) says so.
EXAMPLE: Unary increment (textbook)
-
Alphabet is (B, 1), where B is Blank symbol
-
0 is encoded by 1, 1 is encoded by 11, 2 by 111, 3 by 1111, 4 by 11111,
etc
-
simple algorithm requires only two instructions
-
(1, 1, 1, 1, R) // scan right over the 1’s
-
(1, B, 1, 2, R) // when you reach the right end, replace first blank
with 1.
Can you think of different algorithm to do same
task?
Instruction set can also be expressed using a State
Transition Diagram.
In a State Transition Diagram:
-
Circle represents a state,
-
Arrows represent state transitions.
-
Each arrow also represents one instruction.
-
Arrow is labeled with: current symbol, new symbol and direction.
Example of unary increment:
Example: Unary Addition (textbook)
Assume the two values being added are separated by exactly one blank
(1, 1, B, 2, R) // erase leftmost 1
(2, 1, B, 3, R) // erase second 1 (if no second
1, will halt).
(3, 1, 1, 3, R) // scan first value
(3, B, 1, 4, R) // at end of first value,
replace blank with 1
Example: binary increment and addition
If unary increment and addition seem weenie, here is a web page with Turing
machines to do binary increment and addition:
http://math.hws.edu/TMCM/java/xTuringMachine/.
Example: odd parity (textbook)
Count the number of '1's in a binary string. If there is an odd
number, append a '0' to the end of the string. Otherwise, append
a '1' to the end of the string to assure that the total number of '1's
is odd. Parity bits are used in data communication as a means of
detecting certain transmission errors (an error occurs when a transmitted
'0' is received as a '1' or vice versa).
This can be done in a single left-to-right scan of the input with 3
states. The states are:
1. An even number of '1's have been scanned so far.
2. An odd number of '1's have been scanned so far.
3. finished processing the input
The instructions in English are:
If in state 1 and the input is 0, then write a 0, transition to state
1, and move right.
If in state 1 and the input is 1, then write a 1, transition to state
2, and move right.
If in state 1 and the input is B (end), then write a 1, transition
to state 3, and move right.
If in state 2 and the input is 0, then write a 0, transition to state
2, and move right.
If in state 2 and the input is 1, then write a 1, transition to state
1, and move right.
If in state 2 and the input is B (end), then write a 0, transition
to state 3, and move right.
these translate to:
(1, 0, 0, 1, R)
(1, 1, 1, 2, R)
(1, B, 1, 3, R)
(2, 0, 0, 2, R)
(2, 1, 1, 1, R)
(2, B, 0, 3, R)
At each step until you reach
state 3, exactly one rule applies. Thus, the rules can be listed in any order! Remind you of Prolog?
| Because at each step at most one rule applies, this Turing machine is
deterministic. If the algorithm is written so that two or more
rules may be matched, then the machine is non-deterministic and it
is possible to make incorrect choices since only one rule can be applied
per step. Although it is beyond the scope of this course, there is a technique
for translating any non-deterministic Turing machine into an equivalent
deterministic Turing machine. |
Example to do yourself: even length
Alphabet is 1, plus B for Blank.
Tape input is sequence of 1’s.Tape output will contain
even number of 1’s.
What states/instructions are needed?
More interesting example: even numbers of both
0 and 1.
Alphabet is 0 and 1, plus B for Blank
Tape input is sequence of 0’s and 1’s. Tape
output will contain even number of each.
You’ll need these states:
1. even number of 0’s and even number of 1’s, so
far.
2. even number of 0’s and odd number of 1’s, so
far.
3. odd number of 0’s and even number of 1’s, so
far.
4. odd number of 0’s and odd number of 1’s, so far.
5. finished processing
Here is a set of rules:
(1, 0, 0, 3, R)
(1, 1, 1, 2, R)
(1, B, B, 5, R)
(2, 0, 0, 4, R)
(2, 1, 1, 1, R)
(2, B, 1, 5, R)
(3, 0, 0, 1, R)
(3, 1, 1, 4, R)
(3, B, 0, 5, R)
(4, 0, 0, 2, R)
(4, 1, 1, 3, R)
(4, B, 0, 2, R) -- could also be (4, B, 1, 3, R)
Why did I list two different alternatives for the last rule?
Example: sorting
- Input consists of string of 0’s and 1’s.
- Rearrange if necessary so all 0’s proceed all 1’s.
- There is a sorting applet (works on input of a's and b's) with animated
State Transition Diagram at http://www.btinternet.com/~derek.thompson/Turing2.html
- Strategy: scan right until you find '1' followed by '0', then
swap the '0' and the '1' (replace '0' with '1', move left, replace '1' with
'0') and scan back (left) to the beginning. Repeat this until you
scan the whole string without a swap.
There is a similar problem in Lab 19, exercise 19.3. Its strategy is different:
scan right until you find a '1', then replace it with an 'x', then continue scanning
until you find an '0'. Replace the '0' with '1', then scan left and replace
the 'x' with '0'. Repeat this process until either there are no further
'1's or else there are no '0's to the right of a '1'.
Example: Palindrome Detector
See http://ironphoenix.org/tril/tm/ for a Turing Machine applet
that tests whether the input string (A's and B's) is a palindrome (spelled same forward or backward). Output tape contains either YES or NO.
More on State Transition Diagrams
Also used to specify "finite automata", extremely
useful for pattern recognition
-
limited to one left-to-right scan of input
-
no symbol replacement since no return to this cell
-
thus arrow labels need contain only one value (current input)
Example: You are working on a company project called PAN.
All data files created by PAN software must be named according to this
standard:
1. “P”, followed by…
2. any number of digits, followed by…
3. “.dat”
Here is the state transition diagram corresponding to that standard:
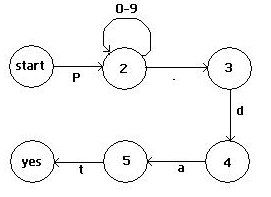
You can now use any file name as input and determine whether or not
the name is valid according to PAN standards. The automaton begins
in the “start” state. Input is valid only if a rule can be applied
for every input character and the automaton finishes in the “yes” state
at the end of the input scan.
Which are valid?
P23.dat
P854N.dat
P.dat
Pete.data
P9832128929390293892913292912.dat
[ C
SC 150 | Peter
Sanderson | Math Sciences server
| Math Sciences home page
| Otterbein ]
Last updated:
Peter Sanderson (PSanderson@otterbein.edu)


