C SC 205 Lecture 15: Balanced Binary Search Trees
major resources: Data Structures and the Java Collections Framework Second Edition, William Collins, McGraw-Hill, 2005
Data Structures and Algorithms in Java Second Edition, Adam Drozdek, Thomson Course Technology, 2005

[ previous | schedule | next ]

Monday November 5 (week 9)

The need for balance

• Balanced means that a tree with N elements has height that is O(log₂N)
• In other words: For any node, the height its left subtrees is close to the height of its right subtree
• You cannot regulate the sequence in which elements will be added to a Binary Search Tree
• If element values are added in a random sequence, the tree will be generally balanced
• If the first element added has a very low or high value, it will be out-of-balance at that level no matter what
• Worst case: element added in ascending or descending value
• In the worst case, adding, removing or locating an element requires linear time.
• In a balanced BST, adding, removing or locating an element requires logarithmic time.

Techniques for maintaining balance

• When can a balanced tree become unbalanced?
• When an element is added
• When an element is removed
• Goal: assure that a balanced tree remains balanced after the add/remove operation
• Different techniques define "balance" differently, but all result in O(log₂n) add/remove/search
• Techniques for maintaining balanced binary search trees
• AVL Tree
• Red-Black Tree
• They have several things in common:
• Each entry (node) has additional information attached
• definitions have requirements that only a balanced tree can meet
• Their add() method differs from BinarySearchTree add in two ways
• include statements to maintain the additional node factoid
• after adding but before returning, call a method to rebalance the tree
• Their remove() method differs from BinarySearchTree remove in the same two ways
• Rebalancing is done through rotation (details below)
• Searching (e.g. getEntry()) is exactly the same as for BinarySearchTree
• Both are introduced in some detail below
• Techniques for maintaining balanced trees (not limited to binary)
• B-tree (similar to Red-Black, but a node may have many children; widely used in database systems)
• 2-3 Tree (every path is same length and all nodes have either 2 or 3 children)
• We will not consider these further
• Here is a simple technique for balancing an arbitrary BST -- but it does not maintain the balance
• Create a temporary array AR with as many elements as are in the tree
• Create a temporary tree TT to hold the balanced tree
• Perform an in-order traversal of BST, placing each element into the first available AR index
• (Note the values in AR will be in ascending order)
• Add elements to TT from AR using this recursive method:
     void balance(E AR[], int first, int last) {
        if (first <= last) {
           int middle = (first + last)/2;
           TT.add(data[middle]);
           balance(data, first, middle-1);
           balance(data, middle+1, last);
        }
     }
• The above method, which I got from Data Structure and Algorithms in Java, Second Edition by Drozdek, will insert elements in "binary search" order, middle index first.
• Assign TT, the balanced tree, back to the original BST variable
• To reiterate: this will not maintain a balanced tree, but simply builds one.

AVL Trees

• Acronym formed from last initials of developers (Adel'son-Vel'skii and Landis, 1962)
• A binary search tree is either empty or for root R
• The height of R's left and right subtrees differ by at most 1
• R's left and right subtrees are both AVL trees
• Balanced is maintained upon adding/removing elements through rotation
  
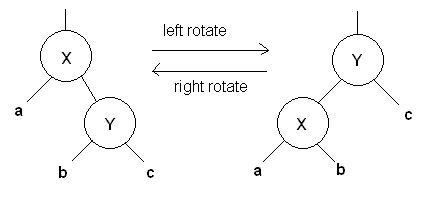
• Left Rotation Rotate a given node X to the left -- X's right child Y takes X's spot and X becomes Y's left child. X adopts Y's existing left child as its new right child.
     X.right = Y.left;
     Y.left = X;
     // Not shown: X's parent replaces X with Y as its left or right child
• Right Rotation Rotate a given node Y to the right -- Y's left child X takes Y's spot and Y becomes X's right child. Y adopts X's existing right child as its new left child.
     X.left = Y.right;
     Y.right = X;
     // Not shown: X's parent replaces X with Y as its left or right child
• Note: Description of right rotation is derived from description of left rotation by exchanging all occurrences of "left" and "right", and "X" and "Y"
• The purpose of left rotation is to reduce height of the right subtree.
• The purpose of right rotation is to reduce height of the left subtree.
• The desired effect doesn't always occur, in which case a double rotation is needed
• Left rotation around X's left child followed by right rotation around X
• Right rotation around X's right child followed by left rotation around X
• The first will reduce height of left subtree.
• The second will reduce height of right subtree.
• Use balance factor to determine when to apply rotation and which rotation to apply.
• balance factor is attached to each node
• = means both its subtrees have same height
• L means its left subtree has greater height (by 1)
• R means its right subtree has greater height (by 1)
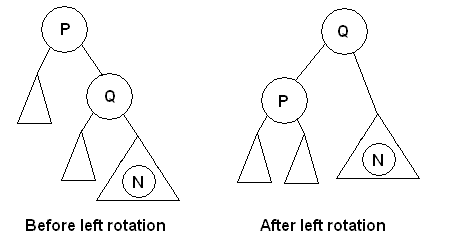
• Rotations when Adding to a tree:
  • Case 1: Suppose new node N is inserted into right subtree of Q. Q is the right child of P and P is the first "unbalanced" ancestor in the path from N to the root. P's balance factor shows its right subtree is higher by 1. This means the new node can "tilt" P's subtree to the right by 2. Re-balance by left rotating Q around P so Q becomes P's parent.
    
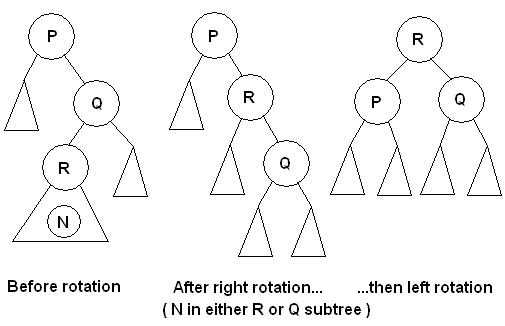
  • Case 2: Suppose new node N is inserted into Q's left subtree, which rooted at Q's left child R. Q is the right child of P and P is the first "unbalanced" ancestor in the path from N to the root. P's balance factor shows its right subtree is higher by 1. This means the new node can "tilt" P's subtree to the right by 2. Re-balance the tree through a double rotation: first rotate right around Q so R becomes Q's parent (this shifts weight toward the right) then rotate left around P so R becomes P's parent.
    
  • Case 3: symmetric to Case 1.
  • Case 4: symmetric to Case 2.
  • (source: Data Structures and Algorithms in Java Second Edition, Adam Drozdek, Thomson Course Technology, 2005)
• Rotation may also be required when an element is removed from the tree.

Red-Black Trees

• Each node has an associated color: Red or Black (analogous to the AVL balance factor)
• A Red-Black tree is a binary search tree which is either empty or root R is Black and
• If an element is Red, none of its children can be Red
• All paths to nodes having less than two children must contain the same number of Black elements. (note that a path includes the nodes at both ends)
• As a consequence of these rules:
• All Red elements will either have 2 children or none (leaf).
• If a Black element has 1 child, it must be a Red leaf.
• No path from a node to the root will contain two Red nodes in a row, but it can contain two Black nodes in a row. So the path colors do not necessarily alternate.
• For a given node, one of its subtrees can have height at most twice the height of the other.
• This is the underlying data structure for the java.util.TreeSet and java.util.TreeMap classes
• See implementation details in source code of java.util.TreeMap
• Nodes are inserted or removed according to BST rules, then after the insertion/removal the tree may violate Red-Black protocal and need to be re-balanced"
• The details for this are found in private TreeMap method fixAfterInsertion() and fixAfterDeletion()
• Fixing a tree requires either a re-coloring of nodes, a rotation or both.
• Textbook author Collins says of the fixAfterInsertion method: "even if you study the code, it makes no sense!"
• For another humorous take on this process, see The Red-Black Tree Song

Useful balanced binary tree that is not a BST: Heap

• Data structure used for Priority Queues
• Priority queue means
  • Each queue element has an associated priority (lower value is higher priority)
  • The dequeue() method will return the queue element having the highest priority
• This is covered in Collins Chapter 13, with a homegrown class.
• We'll just cover the basics.
• A heap is a complete binary tree that is either empty or has root R such that
• R has a smaller value than either of its children
• R's subtrees are themselves heaps
• As a result of the above, the smallest value is always at the root
• Since a heap is required to be a complete binary tree, it is by definition balanced.
• Since it is complete, it can be easily represented by an array
• The enqueue() method adds an entry.
• There is only one to add it, to preserve tree completeness!
• But heap property has to be assured before returning
• Process for assuring this is called percolating up
• While node has greater value than its parent, swap value with parent then recurse up path to root.
• Worst case: have to percolate up to top, but logarithmic since tree is balanced.
• The dequeue() method removes an entry.
• Always removes the value at root, but we can't leave the gap!
• Place value from "last" node (rightmost, lowest level) into the root then delete
• Now the value at the root is large and we need to percolate down
• If root is larger than its children, swap root value with smaller of its children, then recurse on that child.
• Worst case: have to percolate down to the bottom, but logarithmic since tree is balanced.
• Result: enqueue() and dequeue() both are logarithmic time in the worst case.