CSC 150 Chapter 4: The Building Blocks of Computers
primary information resource:
An Invitation to Computer Science (Java), Third Edition,
G. Michael Schneider and Judith L. Gersting,
Course Technology, 2007.
[ previous
| schedule
| next ]
Digital computers are built upon and operate by the simple concept of
on-off.
All data and values are represented and manipulated internally as sequences
of ones and zeroes. On-off.
The streams of ones and zeroes are stored on various memory devices
capable of maintaining two stable physical states. On-off.
The construction of computer circuits is based on Boolean logic, which
has only two possible values, true and false. On-off.
Binary: Characterized by or consisting of two parts or components; twofold
(www.dictionary.com). On-off.
Let's explore these elementary building blocks. You've already
studied some of this in C SC 100.
Binary representation of integer values
-
a.k.a. base 2.
-
the only symbols are 0 and 1.
-
basis for arithmetic: 0+0=0, 0+1=1, 1+0=1, 1+1=10
-
for carries: 0+0+1=1, 0+1+1=10, 1+0+1=10, 1+1+1=11
-
value that each symbol represents depends on its position in the number.
-
each position represents a power of 2. right-most position represents
20
-
second-rightmost position represents 21, third-rightmost represents
22, and so forth.
-
each position is also called a "bit", for BInary-digiT.
-
binary values can easily be converted to decimal (base 10) and vice versa.
-
binary values can most easily be converted to bases which are themselves
powers of 2.
-
computers work internally with fixed-length binary values. This length
itself is a power of 2, usually 32.
-
what happens if result of calculation exceeds 232? overflow,
which can lead to bad things.
-
Give an example where arithmetic operation on two 32 bit values causes
overflow.
Representing negative integer values
-
one solution is designate high-order bit (highest power position) to be
"sign bit". 0=positive, 1=negative.
-
a.k.a. signed magnitude representation.
-
problem: what does value 10000...000 represent? negative zero?
is that the same as 00000...000? Too many questions, not good.
-
A better solution is two's complement. Negative values represented
by starting with binary rep of its absolute value, inverting every bit,
then adding 1 to the result.
-
Sign of two's complement value is still contained in high order bit (1=negative)
-
10000...000 now represents, surprisingly, the largest negative integer.
No more confusing it with zero.
-
1111...111 now represents the smallest negative integer, -1.
-
Another nice feature: to subtract something, just add its two's complement
instead! No special circuitry needed for subtraction.
-
Wanna do some examples using 4-bit values?
Representing real values
-
A scientific notation is used to store numbers with fractional component.
-
Write 'em as: M x BE, where M is the mantissa
(value), E is the exponent and B is the base of the exponent.
-
Example: -98.765 decimal can be written as -98.765 x
100, or -9.8765 x 101, or -.98765 x 102,
or -987.65 x 10-1, or -9876.5 x 10-2, etc.
-
Five components: mantissa, its sign, base, exponent, its sign.
-
We store everything in binary, so the base does not need to be stored (assumed
to be 2).
-
We also normalize the mantissa by adjusting the exponent as necessary
so the decimal point will be positioned just before the first non-zero
digit. Then, the decimal point does not need to be stored either.
-
Normalization is the origin behind the term floating point numbers,
which is used universally in computer science to mean real numbers.
-
As a result, we need store only the mantissa and exponent as signed integer
values.
-
There have been several different standards for floating point numbers
(IEEE 754 now dominates), but all have this in common: a fixed number of
total bits are available (e.g. 64) and within that a fixed number of bits
for each of the mantissa and exponent.
-
Oh, one thing you MUST know about floating point arithmetic -- it is inexact!!
Why? Because many decimal fractions cannot be exactly represented
in binary, particularly given the limit on the mantissa length.
-
Example: the simple decimal fraction 0.1 (one-tenth) if represented by
8 bits yields .00011001 binary (1/62 + 1/32 + 1/256), which translates back to decimal as .09765625,
not even close! The more mantissa bits, the better the approximation,
but it is still not exact.
- Real Example: Decimal fraction 0.1 (1.0 x 10-1) is represented in 32-bit IEEE
754 format as hexadecimal (base 16) 3DCCCCCD. Decimal value 1.0 x 1012
is represented as hexadecimal 5368D4A5. If those values are multiplied,
the result is hexadecimal 51BA43B7, or 9.9999998 x 1010 (equivalent to .99999998 x 1011).
The correct result is 1.0 x 1011.
- More info on IEEE 754:
- This standard defines both 32 and 64 bit floating point representations.
- Both use sign and magnitude.
- The 32 bit representation has 1 sign bit, 8 exponent bits, and 23
mantissa (significand) bits. The 64 bit version has 11 exponent bits and 52 mantissa bits.
- Interpretations of these fields, for 32 bit floating point, are:
- The sign bit is for the overall value,
- The exponent bits represent the true exponent + 127 ("biased" by 127) stored as an unsigned value.
- The mantissa bits
are preceded by an assumed decimal point.
- If the exponent bits are all 0, this is called "denormalized".
- If the exponent bits are a mix of 0's and 1's, this is called "normalized" and an assumed "1" is placed in
front of the assumed decimal point.
- If the exponent bits are all 1, the value is interpreted as either
Infinity (when mantissa is all 0's) or NaN (Not a Number,
when mantissa is not all 0's).
- Because of the sign bit, there are both positive and negative 0.0 and Infinity.
- For more info on IEEE 754, see its Wikipedia entry.
Representing textual values
-
Easy, just devise and use a unique fixed-length bit sequence to represent
each possible character!
-
Character is encoded into this sequence when stored and decoded when read
back.
-
There have been several different standard encodings, the dominant now
are:
-
ASCII, an 8-bit encoding which yields 256 unique characters. Only
the first 128 are in the standard. The rest are assigned willy-nilly
(letters with accents, smiley, text graphics, greek, etc.) by whoever.
Not friendly to large non-latin alphabets.
-
Unicode, a 16-bit encoding which yields 65,536 unique characters.
Java stores text in this format. For more info, see www.unicode.org.
Representing images Digitally
- Binary representation of color
- Value stored in memory represents color.
- How many colors if 1 bit per pixel? what if 8 bits per pixel?
16? 24? 32?
- Bits per pixel is called color depth.
- Screens use RGB color model
- RGB = Red Green Blue
- these are “additive primary colors”
- baseline is black
- assign intensity value to each of the 3 primaries
- intensities of primaries are added to yield resulting color
- Black is zero intensity for all 3 primaries, white is full intensity
of all 3.
- The binary value for a color encodes the 3 intensity values.
- Monitors typically offer 16 bit or 32 bit depth. 32 bit depth is really 24 bits, 8 pits per primary color.
- 8 bits per primary yields 256 intensity levels, and 256 x 256 x 256 = 16.7 million combinations ("true color").
- Color printers based on CMY color model
- CMY = Cyan, Magenta, Yellow
- these are “subtractive primary colors”
- baseline is white
- assign intensity value to each of the 3 primaries
- intensities of primaries are subtracted to yield result.
- Printers really use CMYK, K for black (black ink cartridge rather
than using up the three colors to make black).
- There is a nice demo of these at http://www.phy.ntnu.edu.tw/java/image/rgbColor.html
- There is another demo that shows both additive and subtractive color systems at
http://personal.uncc.edu/lagaro/cwg/Colors/colorBox1.html
- Most web browsers use a "web-safe" palette of 216 colors.
- Screen or printer resolution is dpi (dots per inch).
- Will screen resolution usually match printer resolution? No. Most printers
are at least 300 dpi. Monitors usually less than 100 dpi.
Digital Audio
focus on audio CDs (Compact Discs)
- data on CDs is stored in binary (0's and 1's)
- 0's and 1's are physically recorded by burning, or not burning, pits into reflective metallic surface using a laser
- bits are read from the CD using laser that shines a beam to the CD surface
plus a photo receptor that records how the beam reflects back (to detect pits).
- how does the music get into digital (binary) format?
- original sound is analog - vibrating air.
- Let's do a simple example
- assume a pure sound, the A above middle C, plucked on a guitar
- the reference note A above middle C vibrates as a 440 Hz (Hertz, cycles per second) sine wave
- See
http://www.planetoftunes.com/sound/waveform.html for diagrams illustrating Hertz and sine waves
- See http://www.eminent-tech.com/music/multimediatest.html to play some test tones.
- the sine wave is digitized by measuring its amplitude (strength) as an electrical signal
at regular time intervals then
converting the amplitude to a number using an analog-to-digital converter (ADC).
- Each measurement is called a sample
- It has to be sampled at least two times per cycle to convert back to correct frequency at playback
- To capture a 440 Hz signal requires at least 880 samples per second
- Have to decide how precise each sample should be. How many intervals to define
on the y (vertical) axis of the signal.
- The more precise each sample is, the more bits are required to store its value.
- 256 intervals on vertical axis leads to 8 bits for each sample (can store range 0-255).
- real music is much more complex; waveform represents many different frequencies and signal
strengths combined so it is very "craggy"
- this example, from Roxio Easy CD Creator
(roxio.com), shows a clip from OutKast's "Hey Ya". Top
waveform is left stereo channel; right channel below it. The highlighted section is the phrase "hey ya"
from the chorus
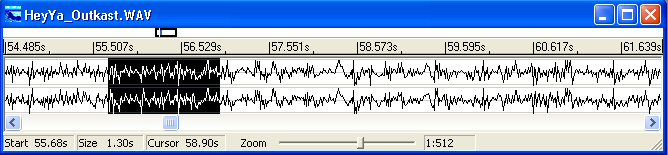
- Music on CDs (uncompressed) is sampled:
- 44,100 samples per second. Can capture signals up to about 22 KHz (kilohertz)
- each sample is 16 bits (2 bytes) long, corresponding to 65536 intervals on the vertical axis
- this means that each second of music generates 88,200 bytes of data per channel
- stereo requires 2 channels, so double that to 176,400 bytes per second, or 10,584,000 bytes per minute of sound (10MB).
- audio CDs can hold up to 80 minutes of audio. This should require about 10 MB x 80 = 800 MB (megabytes).
- each song on standard CD is stored in CDA (CD Audio) format. On a Windows
system, you can discover that their filenames end in ".CDA" (can find
this, using command prompt). It is not compressed.
- By sampling faster, higher frequencies can be recorded but humans cannot hear them.
- By increasing the number of bits per sample, the signal accuracy can be improved.
- Windows WAV format is another uncompressed audio format.
- When I make mix CDs on my computer using Easy CD Creator, it "rips" the original CDA file from the CD
and stores it as a WAV on my hard drive then "burns" the WAV back to a CDA on the CD-R.
- at playback time, the bits are read using a laser as described previously. Each sample then goes
through a digital-to-analog converter (DAC) to convert it back into an electrical signal which is then
amplified and sent through speakers to your ears.
Highcriteria.com's Primer
on PC Audio has good information about some of
these topics. Another reference I used was
How stuff works: CDs and
How stuff works: MP3 files.
In audio and video, concurrent technology development by multiple companies and groups have
lead to format wars. Such wars have been going on for centuries. Examples:
-
French versus British telegraph systems (early 1800s)
- Thomas Edison's cylinder versus Alexander Graham
Bell's platter for sound recordings (late 1800s).
- More recent and most famously, Sony's Beta tape versus
JVC's VHS tape for video cassette recordings.
- The recent hot format war over
competing and incompatible technology for high definition DVD. Toshiba threw in the towel,
announcing in February 2008 that it would cease production of HD-DVD disks. Sony's Blu-ray prevailed.
Data Compression
- Why is this of interest?
- a couple simple data compression techniques
- assign codes to data values. For data values that occur more frequently, assign
a shorter code. Morse code does this. Huffman codes do this.
- long sequences of 0's or long sequences of 1's can be replaced by the sequence length
(encoded in binary).
- These techniques are called lossless compression because no information is
lost during the compression -- they can be "decompressed" back to their original value
- image compression. Here is an interesting demo you can do with Paint Shop Pro:
- Start with image and save in several different formats - bmp, tiff,
gif, jpeg will all yield different sized files
- animation compression: save only the frame-to-frame difference.
- audio compression: What is MP3? What does the MP stand for?
- the name itself is a compression of "MPEG audio layer 3". MPEG=motion picture experts group
- compresses by a factor of almost 11! E.g. 32 MB compresses to about 3
MB. It is pretty complex, though.
- A typical MP3 file requires 128K bits per second of music, or 16K bytes. In other words, 16,384 bytes
per second versus 176,400 (see calculations above) for uncompressed.
- uses perceptual noise shaping, or psychoacoustics, which means it uses characteristics of the human
ear and its interactions with the brain which results in how we perceive sound. Examples:
- if a sound contains both loud and soft components then
we usually hear only the loud one. MP3 will remove the soft one, simplifying the signal.
- If the sound contains two notes that are very close together we will hear only one of them. So
remove the other.
- Very low frequencies are non-directional (that's why you only have one
subwoofer), so do not encode them into both channels.
- After applying psychoacoustic principles, traditional data compression techniques are applied.
- Different parts of a song can be stored at different compression rates, for instance 64K bits per
second rather than 128K, depending on how much compression the techniques above can produce.
- The MPEG standard itself focuses on decoding the compressed signal rather than encoding
the original signal.
Thus a variety of encoding algorithms (of varying "quality") are available.
- Result is "near CD quality". In other words, does not sound quite as good as CD (which is not quite
as good as the original), but the space savings are tremendous.
- The most widely used compression techniques, JPEG for images and MP3 for audio, are both classified
as lossy compression. The compression ratio (uncompressed size / compressed size) for both
is about 10 to 1 (which is very very good), but some information is lost in the compression.
- For compression of data representing text, numbers, computer programs, etc, lossy techniques are not an option. It has to be lossless. ZIP compression
is the most well known of the data compression techniques.
Storage Devices for Binary Data
-
Only requirement is to reliably maintain a bit of information in one of
two stable states and switch between states when required.
-
Most electrical signals have a tendency to drift or be inaccurate, so it
is important to:
-
assign the two signal values to be very far apart (e.g. 0 volts for 0 and
+10 volts for 1)
-
interpret inexact signal correctly (e.g. 2.3 volts means 0 and 7.9 volts
means 1).
-
Magnetic storage devices need to maintain one of two distinctly different
magnetic charges in area designated for storing a bit.
-
Magnetic storage devices are electro-mechanical.
-
Name some magnetic storage devices used in computer systems
-
Magnetic is used for long-term storage due to stability.
-
Electrical is used for short-term storage due to volatility.
-
Transistors are simple electrical devices with no mechanical parts (faster,
don't wear out).
- Basic transistor has two input lines, one output line and an internal switch.
One input line, the control, controls the switch (open,close) and the other,
the collector supplies
the signal that is either propagated to the output, the emitter, or not.
Propagation to the emitter occurs only when the control is closed.
-
Transistors need continuous signal to hold a steady state, but can switch
state almost instantaneously.
-
Integrated Circuits (aka chips) consist of miniature transistors and are
thus electrical (volatile) too.
-
Moore's Law
originally applied to the density of transistors on an Integrated Circuit.
Gordon Moore was a co-founder of Intel.
-
The future for storage seems to lie in optics, quantum physics and biology.
If Transistors are the physical building blocks of computers, gates
are the logical building blocks
-
A gate is a device which transforms a set of binary inputs to a binary
output.
-
In other words, a gate implements a function.
-
Gates are constructed from transistors, although they could be built using
any appropriate technology.
-
We will consider the most elementary gates, those that perform the logical
functions AND, OR and NOT.
-
Boolean logic,
named after George Boole, is the mathematics of the logical values true
and false
-
Binary nature of Boolean logic fits perfectly with the on-off, 0/1 concept.
-
Boolean logic is the logic you apply when programming conditional expressions
for if statements and loops.
-
In Java, relational operators that produce a boolean result are: ==, !=,
>=, <=, <, >.
-
In Java, boolean operators that produce a boolean result are: &&
(and), || (or), ! (not).
-
C and C++ also have these operators.
-
Do not confuse them with these similar bitwise operators &, |, ^,
~, which operate bit-by-bit on values represented internally in binary.
-
(Truth tables, examples, exercises)
-
AND gate takes two binary inputs and produces one binary output.
If both inputs are true the output is true else the output is false.
-
OR gate takes two binary inputs and produces one binary output. If
both inputs are false the output is false else the output is true.
-
NOT gate takes one binary input and produces one binary output. If
the input is true the output is false else the output is true.
- Constructing gates from transistors:
- NOT gate constructed from one transistor. transistor control
line is gate input, power supply signal (transistor collector) is gate output line, transistor emitter tied to ground. If control
line closed (date input 1), current flows through transistor to ground and gate output is 0. If control line open (date input
0), current is blocked from transistor so flows to output line and gate output is 1.
-
AND gate constructed by placing two transistors in series using the two
control lines as gate input. Emitter of second transistor is tied to ground.
Gate output is connected to power supply signal (collector of first transistor) with a NOT gate in between.
- NAND (Not AND) gate is similar to AND except there is no NOT gate. Thus it is a similar construction
and widely used.
-
OR gate constructed by placing two transistors in parallel, combining their
emitters to common ground and using the two control lines as gate input.
Gate output is connected to power supply signal (collector for both transisiters) with NOT gate in between.
- NOR (Not OR) gate is similar to OR except there is no NOT gate. Thus it is a similar construction
and widely used.
Building circuits from gates
-
A circuit is a set of gates which transforms binary inputs to binary outputs.
-
It is the next level of hardware abstraction in the progression: transistors
-> gates -> circuits.
-
Circuits perform higher-level and more complex operations such as addition
and comparison
-
A circuit is the physical equivalent of Boolean expressions which contain
only Boolean operators (one expression per output line)
-
Circuit specification can be represented either by Boolean expression(s)
or circuit diagram.
Process for designing circuits (without optimization)
1. construct truth table (complete input to output transformation,
each column represents a bit)
2. for each output column
(a) for each output row containing 1, build AND expression combining
inputs in that row (first applying NOT on any 0 inputs)
(b) combine all the AND expressions created in 2a with ORs
(c) construct circuit diagram from resulting Boolean expression.
3. combine the circuit diagrams
Example: output is count of the number of 1's in the input.
input | output
a b c | d e
--------+------
0 0 0 | 0 0
0 0 1 | 0 1
0 1 0 | 0 1
0 1 1 | 1 0
1 0 0 | 0 1
1 0 1 | 1 0
1 1 0 | 1 0
1 1 1 | 1 1
output d: (!a && b && c) || (a
&& !b && c) || (a && b && !c) ||
(a && b && c)
output e: (!a && !b && c) || (!a &&
b && !c) || (a && !b && !c) || (a && b
&& c)
(drew circuit using lab software)
optimization results in fewer gates (cheaper, smaller, less power, less
heat)
Example:
input | output
a b | c
-------+------
0 0 | 0
0 1 | 0
1 0 | 1
1 1 | 1
step 2 results in boolean expression: (a && !b) ||
(a && b)
This can be reduced to simply: a
(reduced from 4 gates to none)
[ C
SC 150 | Peter
Sanderson | Math Sciences server
| Math Sciences home page
| Otterbein ]
Last updated:
Peter Sanderson (PSanderson@otterbein.edu)
